zadanie 32.1 (0-2) zbiór rozszerzenie

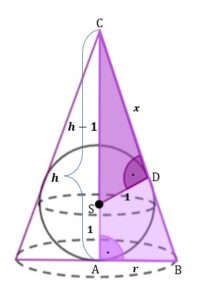
Zaznaczymy na obrazku kąty proste jakie tworzy promień kuli z podstawą stożka oraz jaki tworzy promień kuli z tworzącą stożka. Zaznaczymy jednocześnie na naszym obrazku trójkąty prostokątne które będą do siebie podobne.

Oznaczymy przez $h$ wysokość stożka oraz oznaczymy wierzchołki trójkątów prostokątnych podobnych.

Możemy zapisać długości odcinków:

$\left | AB \right |=r$

$\left | AC \right |=h$

$\left | SC \right |=h-1$

$\left | SA \right |=\left | SD \right |=1$

oraz oznaczmy $\left | CD \right |=x$

Z twierdzenia Pitagorasa z trójkąta $SDC$ mamy:

$1^2+x^2=\left ( h-1 \right )^2$

$x^2=h^2-2h+1-1$

$x=\sqrt{h^2-2h}$

Korzystając z podobieństwa trójkątów $ABC$ i $DSC$ możemy zapisać:

$\frac{\left | AB \right |}{\left | AC \right |}=\frac{\left | SD \right |}{\left |DC \right |}$

$\frac{r}{h}=\frac{1}{x}$

$\frac{r}{h}=\frac{1}{\sqrt{h^2-2h}}$

$r\cdot \sqrt{h^2-2h}=h\cdot 1\; \; /:\sqrt{h^2-2h}$

$r=\frac{h}{\sqrt{h^2-2h}}$

$r=\sqrt{\frac{h^2}{h\left ( h-2 \right )}}$

$r=\sqrt{\frac{h}{h-2}}$

Wyznaczmy funkcje opisująca objętość stożka uzależnioną od długości jego wysokości

$V(h)=\frac{1}{3}\pi\cdot \left ( \sqrt{\frac{h}{h-2}} \right )^2\cdot h$

$V(h)=\frac{1}{3}\pi\cdot\frac{h}{h-2} \cdot h$

$V(h)=\frac{h^2\pi }{3\left ( h-2 \right )}$

Co należało pokazać.

Was this helpful?

1 / 0

Dodaj komentarz 0