zadanie 32.2 (0-5) zbiór rozszerzenie

Korzystamy z wzoru na objętość

$V(h)=\frac{h^2\pi }{3\left ( h-2 \right )}$

Ustalmy dziedzinę funkcji $V$

$h>0\; \; \wedge \; \; h-2>0\; \; \wedge \; \; h-2\neq 0$

$h>0\; \; \wedge \; \; h>2\; \; \wedge \; \; h\neq 2$

$h\in \left ( 2,+\infty \right )$

$D_{V}:h\in \left ( 2,+\infty \right )$

Obliczymy teraz pochodną i jej miejsca zerowe

$V'(h)=\frac{2h\pi \cdot 3\left ( h-2\right )-3\cdot h^2\pi }{\left [3\left ( h-2 \right ) \right ]^2}=\frac{6h^2\pi -12h\pi -3 h^2\pi }{9\left ( h-2 \right )^2}$

$V'(h)=\frac{3h^2\pi -12h\pi }{9\left ( h-2 \right )^2}=\frac{3h\pi \left (h -4\right ) }{9\left ( h-2 \right )^2}$

$V'(h)=\frac{h\pi \left (h -4\right ) }{3\left ( h-2 \right )^2}$

$V'(h)=0\; \; \Leftrightarrow \; \;\frac{h\pi \left (h -4\right ) }{3\left ( h-2 \right )^2}=0$

$\frac{h\pi \left (h -4\right ) }{3\left ( h-2 \right )^2}=0\; \; /\cdot 3\left ( h-2 \right )^4$

$h\pi \left ( h-4 \right )\left ( h-2 \right )^2=0$

$h\pi =0\; \; /:\pi \; \; \vee\; \; h-4=0\; \; \vee \; \; \left (h-2 \right )^2=0$

$h =0 \; \; \vee\; \; h=4\; \; \vee \; \; h=2$

$V'(h)>0\; \; \Leftrightarrow \; \; h\in\left ( 4,+\infty \right )$

$V'(h)<0\; \; \Leftrightarrow \; \; h\in\left (2,4 \right )$

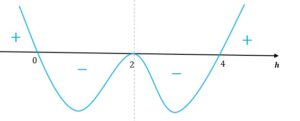Funkcja $V(h)$ rośnie w przedziale $h\in \left [ 4,+\infty \right )$ oraz maleje w przedziale $h\in \left ( 2,4 \right ]$ . Zatem w punkcie $h=4$ funkcja osiąga najmniejszą wartość (minimum). Objętość ta jest wówczas równa:

$V\left ( 4 \right )=\frac{4^2\pi }{3\left ( 4-2 \right )}=\frac{16\pi }{3\cdot 2}$

$V\left ( 4 \right )=\frac{8\pi }{3}$

Was this helpful?

0 / 0

Dodaj komentarz 0