Liczba naturalna, która dzieli się tylko przez 1 i przez sama siebie jest liczbą pierwszą. A co kiedy liczba naturalna ma więcej niż te dwa dzielniki? Wówczas każdą taką liczbę nazywamy liczbą złożoną. Musimy pamiętać, że ani 0, ani 1 nie są liczbami pierwszymi i nie są też liczbami złożonymi.
Spróbujmy ze zbioru kilku początkowych liczb naturalnych wybrać kilka liczb pierwszych i kilka złożonych, wypisując obok nich dzielniki
| liczba naturalna | pierwsza/ złożona | dzielniki |
| 2 | pierwsza | 1, 2 |
| 3 | pierwsza | 1, 3 |
| 4 | złożona | 1, 2, 4 |
| 5 | pierwsza | 1, 5 |
| 6 | złożona | 1, 2, 3, 6 |
| 7 | pierwsza | 1,7 |
| 8 | złożona | 1, 2, 4, 8 |
| 9 | złożona | 1, 3, 9 |
| 10 | złożona | 1, 2, 5, 10 |
| 11 | pierwsza | 1, 11 |
Warte zapamiętania jest to, że 2 jest jedyną liczba pierwszą parzystą. Co do nieparzystych liczb pierwszych jest ich nieskończenie wiele i co jakiś czas, ktoś podaje nową bardzo dużą liczbę pierwszą.
Rozkład liczby naturalnej na czynniki pierwsze to zapisanie tej liczby w postaci iloczynu liczb pierwszych (od najmniejszej do największej). Jak to zrobić? A więc bierzemy dowolną liczbę naturalną na przykład 138 i zapisujemy ją w postaci iloczynu (nie koniecznie liczb pierwszych), czyli 138 = 2 · 69. Następnie próbujemy rozłożyć liczbę złożoną z naszego iloczynu, czyli 69 na iloczyn liczb naturalnych i tak dalej, aż finalnie dojdziemy do iloczynu, który składa się z samych liczb pierwszych. W naszym przypadku 128 = 2 · 3 · 23
Jest jeszcze inna metoda, znajdywania rozkładu liczby na czynniki pierwsze i z doświadczenia wiem, że uczniowie wolą z niej korzystać. Weźmy sobie liczbę 168 i rozłóżmy ją na czynniki naturalne.
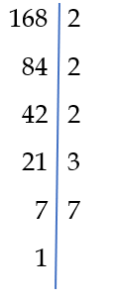
Jak widać zaczynamy od znalezienia najmniejszej liczby pierwszej, która dzieli naszą liczbę naturalną. Wynik zapisujemy pod naszą liczbą i znowu szukamy najmniejszej naturalnej liczby dzielącej otrzymaną liczbę i tak dalej, aż dochodzimy do 1. Spisując iloczyn liczb znajdujących się po prawej stronie kreski, otrzymujemy rozkład liczby na czynniki pierwsze.
168= 2 · 2 · 2 · 3 · 7
Spróbujmy rozłożyć jeszcze jedną liczbę naturalną na czynniki pierwsze. Na przykład 2310:
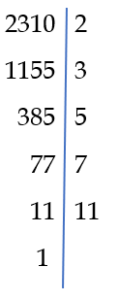
czyli nasz rozkład będzie wyglądał następująco:
2310 = 2 · 3 · 5 · 7 · 11
Jeszcze jedna bardzo ważna informacja musimy sobie uświadomić, że rozkład na czynniki naturalne jest jednoznaczny. Co to znaczy? To znaczy, że aby zapisać taki rozkład, nie można użyć innych liczb pierwszych niż te, które tworzą dany rozkład liczby na czynnik pierwsze. Oczywiście możemy liczby pierwsze zapisać w innej kolejności, ale wiadomo, że mnożenie jest przemienne i nic to nie zmieni.
Jeśli już umiemy wyznaczyć rozkład liczby na czynniki naturalne możemy sobie ułatwić szukanie największego wspólnego dzielnika NWD lub najmniejszej wspólnej wielokrotności NWW dwóch liczb.
Weźmy dwie dowolne liczby naturalne 120 i 924 i rozłóżmy je na czynniki pierwsze:
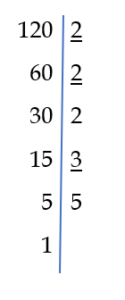
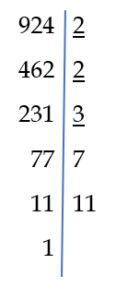
Największy wspólny dzielnik, to iloczyn powtarzających się dzielników (podkreślone liczby)
NWD( 120, 924 ) = 2 · 2 · 3 = 12
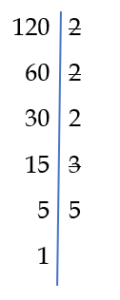
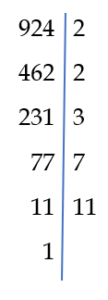
Najmniejszą wspólną wielokrotność wyznaczamy wykreślając w rozkładzie mniejszej liczby te dzielniki, które występują w rozkładzie większej liczby i mnożymy większą liczbę przez te dzielniki, które nie zostały skreślone w liczbie mniejszej.
NWW(120 , 924) = 924 · 2 · 5 = 9240
Was this helpful?
5 / 7