Ułamki zwykłe - Matma.com.pl

Pewnie nie każdy wie, że ułamkami posługiwano się w starożytności tylko trochę inaczej je zapisywano. licznik był na dole, mianownik na górze i nie było kreski ułamkowej. Dla nas to trochę dziwny zapis, ale jak widać znajomość ułamków jest potrzebna w życiu i już w dawnych czasach nie potrafili sobie bez nich poradzić.

Ułamki zwykłe

Ułamek, czyli inaczej mówiąc cześć całości. Musimy sobie jednak uświadomić, że ułamek jest liczbą, która przedstawia jakąś wartość i można ją porównywać z innymi liczbami. A ponieważ jest to liczba to ma swoje miejsce na osi liczbowej.

Zacznijmy od tego jak wygląda ułamek zwykły

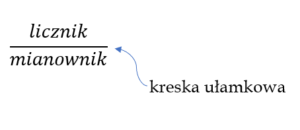
kreska ułamkowa to nic innego jak znak dzielenia („:”) czyli ułamek $\frac{5}{8}{\color{DarkBlue} }$ oznacza 5 : 8. Ułamek to inaczej iloraz dwóch liczb.

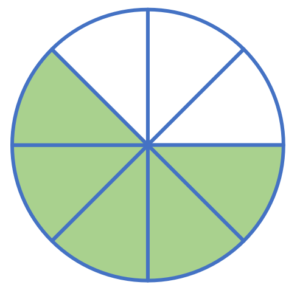
Spróbujmy ten ułamek (zielony kolor) przedstawić za pomocą rysunku:

Możemy zaznaczyć nasz ułamek na osi liczbowej:

Pamiętamy, że każdą liczbę naturalną możemy zapisać w postaci ułamka, mianowicie $1=\frac{2}{2}=\frac{3}{3}=\frac{4}{4}= ...$ lub $5=\frac{10}{2}=\frac{15}{3}=\frac{20}{4}= ...$

Jeśli licznik jest mniejszy od mianownika, na przykład $\frac{3}{7}$ wtedy ułamek nazywamy ułamkiem właściwym. Natomiast gdy licznik jest większy od mianownika, na przykład $\frac{7}{4}$ wtedy ułamek nazywamy ułamkiem niewłaściwym.

Każdy ułamek niewłaściwy możemy zamienić na liczbę mieszaną, czyli liczbę zawierającą cześć całkowitą oraz część ułamkową na przykład:

$\frac{7}{4}=\frac{4+3}{4}=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4 }=1\frac{3}{4}$

lub jak ktoś woli: $7:4=1\, reszty\, 3 = 1\frac{3}{4}$ (to już jak komuś wygodniej).

Oczywiście każdą liczbę mieszaną możemy zamienić na ułamek niewłaściwy, na przykład $6\frac{3}{5}=\frac{6\cdot 5+3}{5}=\frac{33}{5}$ .

Każdy ułamek da się rozszerzyć mnożąc licznik i mianownik przez tę samą liczbę, oczywiście różną od zera, np. $\frac{2}{3}=\frac{2\cdot 5}{3\cdot 5}=\frac{10}{15}$ . Musimy pamiętać, że po rozszerzeniu wartość ułamka się nie zmienia. Możemy skrócić ułamek dzieląc jego licznik i mianownik przez ich wspólny dzielnik na przykład:

$\frac{25}{30}=\frac{25:5}{30:5}=\frac{5}{6}$ .

Należy jednak pamiętać, że nie wszystkie ułamki da się skrócić, wtedy mamy do czynienia z ułamkami nieskracalnymi na przykład $\frac{13}{15}$ .

Jak sprawdzić, który ułamek jest większy, a który mniejszy?

Jeśli ułamki mają takie same liczniki to większy jest ten, który ma mniejszy mianownik;

$\frac{4}{9}< \frac{4}{7}$ lub $\frac{1}{2}> \frac{1}{3}$

Jeśli ułamki mają takie same mianowniki to większy jest ten, który ma większy licznik;

$\frac{7}{11}> \frac{5}{11}$ lub $\frac{3}{7}< \frac{6}{7}$

Jeśli ułamki mają różne liczniki i mianowniki to trzeba sprowadzić je do wspólnego mianownika (oba ułamki muszą mieć jednakowe mianowniki) i wtedy porównać ułamki;

Co jest większe $\frac{2}{3} \,\, czy \, \, \frac{3}{4}$ ?