zbiór zadań rozszerzenie CKE

zadanie 1 (0-3)

Oblicz wartość wyrażenia

$\log _{8}3^{3\log _{3}2-\log _{27}8-\log _{9}4}$

Zapisz obliczenia.

zadanie 2 (0-4)

Liczby $a,b,c$ są kolejnymi wyrazami ciągu arytmetycznego o różnicy równej $7$ . Jedna z tych liczb jest wielokrotnością liczby $7$ .

Wykaż, że iloczyn $a\cdot b\cdot c$ jest podzielny przez $294$ .

ROZWIĄZANIE

zadanie 3 (0-2)

Niech $a,b$ będą liczbami całkowitymi, dla których zachodzi równość $2a^2+a=3b^2+b$ .

Wykaż, że jeśli $5$ jest dzielnikiem liczby $a-b$ , to $25$ również jest dzielnikiem liczby $a-b$ .

ROZWIĄZANIE

zadanie 4 (0-2)

Rozpatrzmy liczby naturalne większe od $1000$ , w których zapisie występuje tylko cyfra $1$ :

$\begin{matrix}a= \underbrace{11...111}\\ \; \; \; \;\; \; n\end{matrix}$

Wykaż, że jeśli liczba $a$ zapisana za pomocą $n$ jedynek jest liczbą pierwszą, to liczba $n$ również jest liczbą pierwszą.

ROZWIĄZANIE

zadanie 5 (0-4)

Suma liczb całkowitych $x$ i $y$ jest podzielna przez $3$ .

Wykaż, że suma sześcianów liczb $x$ i $y$ jest podzielna przez $9$ .

ROZWIĄZANIE

zadanie 6 (0-3)

W rozwinięciu wyrażenia $\left ( a+b \right )^n$ dla pewnego $n\in \mathbb{N}$ suma współczynników przy wyrazach $a^{n-2}b^2$ oraz $a^{n-1}b$ jest równa 66.

Oblicz $n$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 7 (0-3)

Niech $a,b,c$ będą takimi liczbami całkowitymi, że $a\sqrt{2}+b\sqrt{3}+c\sqrt{6}=0$

Wykaż, że $a=b=c=0$ .

ROZWIĄZANIE

zadanie 8 (0-3)

Wykaż, że liczba $a=\left ( \sqrt{5} +2\right )^{2022}+\left ( \sqrt{5} -2\right )^{2022}$ jest wymierna.

ROZWIĄZANIE

zadanie 9 (0-3)

Rozwiąż nierówność $2x^2+x\left | 2x-1 \right |\leq 3$ .

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 10 (0-5)

Rozwiąż nierówność

$x+4+\frac{8}{x-4}\geq \frac{-2x-8}{x^2-16}$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 11 (0-4)

Wyznacz wszystkie wartości parametru $m$ , dla których równanie

$2x^2-\left ( 2m+7 \right )x+m^2-3m+21=0$

ma dwa różne rozwiązania rzeczywiste $x_{1}$ oraz $x_{2}$ , spełniające warunek $x_{1}=2x_{2}$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 12 (0-2)

Wykaż, że dla każdej liczby naturalnej $n$ prawdziwe są nierówności

$2\left ( \sqrt{n+2}-\sqrt{n+1} \right )< \frac{1}{\sqrt{n+1}}$ i $\frac{1}{\sqrt{n+1}}< 2\left ( \sqrt{n+1}-\sqrt{n} \right )$

ROZWIĄZANIE

zadanie 13 (0-3)

Rozwiąż układ równań

$\left\{\begin{matrix} x^2-2x+y^2=24\\x^2-8x+y^2-10x+40=0 \end{matrix}\right.$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 14 (0-3)

Dane są funkcję $k$ oraz $p$ . Funkcja $k$ jest określona wzorem $k(x)=5-x^2$ dla każdej liczby rzeczywistej $x$ . Funkcja $p$ jest określona wzorem $p(x)=\sqrt{1-x}$ dla każdej liczby rzeczywistej $x$ nie większej od $1$ . Funkcje $f$ oraz $g$ są określone następująco:

$f=k\circ p$ oraz $g=p\circ k$

Wyznacz wzory i dziedziny funkcji $f$ oraz $g$ .

ROZWIĄZANIE

zadanie 15 (0-4)

Narysuj wykres funkcji $f(x)=\frac{\left | x^2-9 \right |}{3-x}$ .

Wyznacz wszystkie wartości parametru $m$ , dla których równanie $f(x)=m$ nie ma rozwiązania. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 16 (0-5)

Dany jest rosnący ciąg arytmetyczny $\left ( a_{n} \right )$ określony dla każdej liczby naturalnej $n\geq 1$ . Ciąg $\left ( a_{1}\cdot a_{2} ,a_{2}\cdot a_{3},a_{1}\cdot a_{3}\right )$ jest geometryczny i ma wyrazy różne od zera.

Oblicz iloraz tego ciągu geometrycznego. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 17 (0-2)

Na płaszczyźnie, w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dane są dwie proste $l_{1}$ oraz $l_{2}$ . Kąt między tymi prostymi ma miarę $45^\circ$ . Współczynnik kierunkowy w równaniu prostej $l_{1}$ jest równy $\frac{2}{3}$

Oblicz współczynnik kierunkowy w równaniu prostej prostej $l_{2}$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 18 (0-5)

Rozwiąż równanie

$\cos ^{2}x-\frac{2\sqrt{3}}{3}\sin x\cos x-\sin ^{2}x=0$

w przedziale $\left [ -\pi ,\pi \right ]$ .

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 19 (0-3)

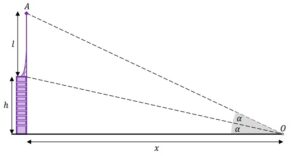Na szczycie wieży o wysokości $h$ umieszczono pionowo antenę radiową stacji nadawczej o długości $l$ $\left ( l> h \right )$ . Punkt $O$ leży na płaszczyźnie poziomej przechodzącej przez podnóże wieży, a punkt $A$ znajduje się na końcu anteny. Koniec anteny $A$ widać z punktu $O$ pod dwukrotnie większym kątem niż wieżę (zobacz rysunek)

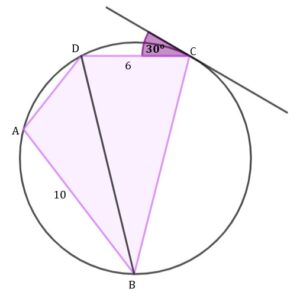
Oblicz odległość $x$ podnóża wieży od punktu $O$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 20 (0-6)

Oblicz pole czworokąta $ABCD$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 21 (0-4)

W trapezie $ABCD$ przekątna $BD$ jest dwusieczną kąta $CBA$ i przecina przekątną $AC$ w punkcie $K$ , takim że $\left | CK \right |:\left | KA \right |=1:3$ . Pole tego trapezu jest równe $100\left ( \sqrt{6} -\sqrt{2}\right )$ , $\sin \measuredangle BAD=\frac{\sqrt{6}+\sqrt{2}}{4}$ , $\left | AD \right |=10$ oraz kąt $BAD$ jest ostry.

Oblicz długość pozostałych boków trapezu $ABCD$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 22 (0-6)

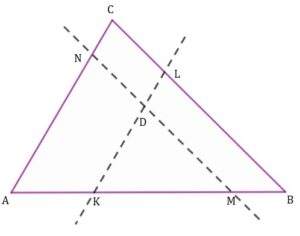Punkt $D$ leży wewnątrz trójkąta $ABC$ . Prosta przechodząca przez punkt $D$ i równoległa do boku $AC$ , przecina bok $AB$ w punkcie $K$ a bok $BC$ w punkcie $L$ . Prosta przechodząca przez punkt $D$ i równoległa do boku $BC$ przecina bok $AB$ w punkcie $M$ , a bok $AC$ w punkcie $N$ (zobacz rysunek). Stosunek obwodu trójkąta $KMD$ do obwodu trójkąta $KBL$ jest równy $5:7$ , a stosunek obwodu trójkąta $KMD$ do obwodu trójkąta $AMN$ jest równy $5:8$ . Pole czworokąta $DLCN$ jest równe $15$

Oblicz pole trójkąta $ABC$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 23 (0-3)

Funkcja $f$ jest określona wzorem

$f(x)=\frac{\sqrt{2x}}{5+x^2}-3^{-x-1}$

dla każdej nieujemnej liczby rzeczywistej $x$ .

Wykaż, że funkcja $f$ ma co najmniej jedno miejsce zerowe dodatnie mniejsze od $3$ .

ROZWIĄZANIE

zadanie 24 (0-3)

Funkcja $f$ jest określona wzorem $f(x)=\sqrt{1+4x}$ dla $x\in \left [ -\frac{1}{4} ,+\infty \right )$

Napisz równanie stycznej do wykresu funkcji $f$ w punkcie $x_{0}=2$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 25 (0-4)

Funkcja $f$ jest określona wzorem $f(x)=x^4-2x^3+x^2-1$ dla każdej liczby rzeczywistej $x\in \left [ -1,3 \right ]$

Wyznacz zbiór wartości funkcji $f$ .

ROZWIĄZANIE

zadanie 26 (0-3)

Trójkąt $ABC$ , w którym $\left | AC \right |=\left | BC \right |$ , jest wpisany w okrąg o promieniu $R$ . Środek tego okręgu leży wewnątrz trójkąta $ABC$ . Niech $x$ oznacza odległość środka okręgu od podstawy $AB$ .

Wykaż, że pole trójkąta $ABC$ jako funkcją zmiennej $x$ jest określone wzorem $P(x)=\left (R+x \right )\sqrt{R^2-x^2}$ . Określ dziedzinę tej funkcji.

ROZWIĄZANIE

zadanie 27 (0-6)

Dany jest okrąg o promieniu $R$ . Rozważmy wszystkie trójkąty spełniające warunki:

są wpisane w ten okrąg
mają obwody równe $3R$
mają jeden z boków dwukrotnie dłuższy od drugiego.

Znajdź trójkąt o możliwie największym polu przy zadanych warunkach. Oblicz jego pole. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 28 (0-6)

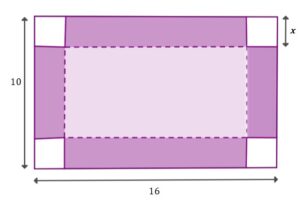Grażyna planuje zrobienie pudełka (bez wieczka) w kształcie prostopadłościanu. W tym celu zamierza wykorzystać prostokątny kawałek tektury o wymiarach $10\: \mathrm{cm}\times 16\: \mathrm{cm}$ , odcinając z każdego rogu kwadrat o boku $x$ cm (zobacz rysunek).

Oblicz wartość $x$ , dla której objętość otrzymanego pudełka będzie największa. Oblicz tę największą objętość pudełka. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 29 (0-6)

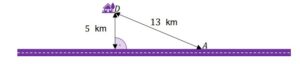Dom $D$ stoi w odległości $5\; \mathrm{km}$ od prostoliniowego odcinka drogi. W chwili początkowej Janusz znajduje się na tej drodze w punkcie $A$ oddalonym od domu $D$ o $13\; \mathrm{km}$ (zobacz rysunek). Janusz może iść drogą z maksymalną prędkością $5\; \mathrm{km/h}$ , zaś poza nią może poruszać się z maksymalną prędkością $3 \; \mathrm{km/h}$ .

Oblicz najkrótszy czas potrzebny Januszowi na dojście do domu $D$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 30 (0-4)

Ciężarówka ma do pokonania trasę długości $S$ km, poruszając się po autostradzie ze stałą prędkością $v\; \mathrm{km/h}$ . Minimalna prędkość dla ciężarówki na autostradzie wynosi $40\; \mathrm{km/h}$ , maksymalna – $80\; \mathrm{km/h}$ . Wiemy, że litr paliwa kosztuje $8$ złotych, a kierowca otrzymuje $42$ złote za godzinę swej pracy. Zużycie paliwa w ciągu jednej godziny jazdy autostradą w zależności od prędkości $v$ wyrażone w litrach można opisać funkcją $f(v)=7+\frac{v^2}{400}$ .

Oblicz przy jakiej prędkości koszt przejazdu będzie najmniejszy. Zapisz obliczenia.

Wskazówka: przyjmij, że koszt przejazdu jest sumą kosztu paliwa oraz wynagrodzenia kierowcy.

ROZWIĄZANIE

zadanie 31 (0-6)

Dana jest kula o promieniu $1$ . Rozpatrujemy wszystkie stożki zawierające środek kuli i wpisane w tę kulę, to znaczy takie w których:

wierzchołek leży na powierzchni kuli
okrąg, będący krawędzią podstawy stożka, leży na powierzchni kuli (zobacz rysunek)

Oblicz promień podstawy stożka, który ma największą objętość.

Oblicz objętość tego stożka. Zapisz obliczenia.

ROZWIĄZANIE

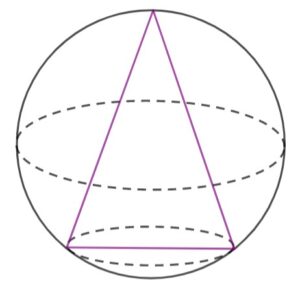
zadanie 32

Dana jest kula o promieniu $1$ . Rozpatrujemy wszystkie stożki opisane na tej kuli, to znaczy takie, których:

podstawa ma dokładnie jeden punkt wspólny z kulą
każda tworząca ma dokładnie jeden punkt wspólny z kulą (zobacz rysunek)

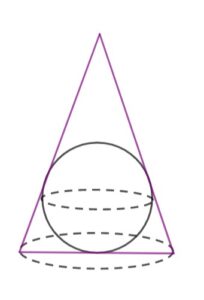zadanie 32.1 (0-2)

Wykaż, że objętość $V$ stożka o wysokości $h$ wyraża się wzorem:

$V(h)=\frac{h^2\pi }{3\left (h-2 \right )}$

ROZWIĄZANIE

zadanie 32.2 (0-5)

Oblicz wysokość tego stożka, który ma najmniejszą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.

Wskazówka: skorzystaj z informacji, że objętość stożka o wysokości $h$ wyraża się wzorem

$V(h)=\frac{h^2\pi }{3\left (h-2 \right )}$

ROZWIĄZANIE

Was this helpful?

3 / 6