zbiór zadań podstawa CKE

zadanie 1 (0-2)

Wykaż, że suma trzech kolejnych liczb całkowitych jest podzielna przez 3.

zadanie 2 (0-1)

Liczbę $a=\left ( \sqrt{2} +\sqrt{7}\right )^{2}$ można zapisać w postaci $a=x+y\sqrt{14}$ , gdzie $x\in \mathbb{Z}$ oraz $y\in \mathbb{Z}$ .

Uzupełnij poniższe równości. Wpisz właściwe liczby w wykropkowanych miejscach.

$x=................$

$y=................$

ROZWIĄZANIE

zadanie 3 (0-3)

Rozważmy takie liczby $a$ i $b$ , które spełniają warunki:

$a\neq 0$ oraz $b\neq 0$ oraz $a\sqrt{2}+b\sqrt{3}=0$

Oblicz wartość liczbową wyrażenia $\frac{a}{b}+\frac{b}{a}$ dla dowolnych liczb rzeczywistych $a$ i $b$ , spełniających powyższe warunki. Wynik podaj w postaci ułamka bez niewymierności w mianowniku.

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 4 (0-2)

Dana jest liczba

$a=\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}$

Wykaż, że $a$ jest liczba całkowitą. Zapisz obliczenia.

Wskazówka: Usuń niewymierności z mianowników.

ROZWIĄZANIE

zadanie 5 (0-1)

Która z podanych równości (A-D) jest prawdziwa. Wybierz właściwą odpowiedź spośród podanych.

A. $\left ( \sqrt{7}+\sqrt{5} \right )^{3}=\sqrt{7^{3}}+\sqrt{5^{3}}$	B. $\sqrt{\sqrt{144}+\sqrt{16}}=2^{\frac{4}{2}}$
C. $\left ( 2\frac{1}{4} \right )^{3}=2^{\frac{3}{2}}+\left ( \frac{1}{2} \right )^{3}$	D. $\left (\sqrt[3]{64} \right )^{\frac{1}{8}}=8^{3}$

ROZWIĄZANIE

zadanie 6 (0-2)

Okres $T$ drgań wahadła w pewnym zegarze dany jest wzorem:

$T=2\pi\sqrt{\frac{l}{g}}$

gdzie $l$ oznacza długość wahadła, a $g$ oznacza przyspieszenie grawitacyjne. Przyjmij do obliczeń, że przyspieszenie grawitacyjne na Ziemi wynosi $g_{z}=9,81\; m/s^2$ , a przyspieszenie grawitacyjne na Księżycu wynosi $g_{k}=1,62\; m/s^2$ .

Oblicz $\frac{T_{k}}{T_{z}}$ – stosunek okresu drgań tego wahadła, gdyby znajdowało się ono na księżycu, do okresu drgań tego samego wahadła znajdującego się na Ziemi. Wynik podaj z dokładnością do 0,01.

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 7 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość wyrażenia $\log k+\log \frac{1}{100}k^2-\log \frac{1}{10}k^3$ , gdzie $k>0$ , jest równa

A. $0$

B. $1$

C. $(-1)$

D. $k$

ROZWIĄZANIE

zadanie 8 (0-2)

Liczby rzeczywiste $x,y,z$ spełniają następujące warunki:

$x,y,z>0$ oraz $x,y,z\neq 1$ oraz $y^z=x$

Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.

Z podanych warunków wynika, że prawdziwe są nierówności:

A. $\log _{x}y=z$	B. $y^{-\log _{y}x}=\frac{1}{x}$
C. $\log _{x}z=y$	D. $y^{\log _{x}y}=x$
E. $\log _{y}x=z$	F. $z^{-\log _{x}y}=\frac{1}{z}$

ROZWIĄZANIE

zadanie 9 (0-1)

Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F- jeśli jest fałszywe.

Wyrażenie $2x^2-1$ można przekształcić równoważnie do wyrażenia $\left ( 1-x\sqrt{2} \right )\left (x\sqrt{2} -1\right )$ .	P	F
Dla każdej liczby rzeczywistej $x$ wartość wyrażenia $\left ( 2+x \right )^3-x^2\left ( x+6 \right )-12x=8$	P	F

ROZWIĄZANIE

zadanie 10 (0-1)

Dany jest wielomian:

$W(x)=x^3-9x^2+26x-24$

który ma trzy pierwiastki całkowite.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Jednym z pierwiastków tego wielomianu jest liczba

A. $13$

B. $12$

C. $7$

D. $2$

ROZWIĄZANIE

zadanie 11 (0-3)

Dane jest wyrażenie:

$\left ( \frac{a}{a+b}-\frac{a^2}{a^2-b^2} \right ):\left ( \frac{a-b}{a^2-b^2} \right )$

gdzie $a\in \mathbb{R},b\in \mathbb{R}$ , $a\neq b$ , $a\neq- b$ .

Przekształć dane wyrażenie do najprostszej postaci i oblicz jego wartość dla $a=\frac{2}{\sqrt{3}}$ oraz $b=-\frac{1}{\sqrt{3}}$ .Zapisz obliczenia.

ROZWIĄZANIE

zadanie 12 (0-2)

Wyrażenie wymierne $\frac{2}{x-3}+5$ można przekształcić równoważnie do wyrażenia $\frac{ax+b}{cx+d}$ , gdzie $a,b,c,d$ są pewnymi współczynnikami rzeczywistymi.

Wyznacz wartości liczbowe współczynników $a,b,c,d$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 13 (0-1)

Dany jest wielomian

$W(x)=x^3-4x^2+x+6$ gdzie $x\in \mathbb{R}$

Dokończ zdanie tak aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.

Wskazówka: Skorzystaj z podzielności wielomianu $W(x)$ przez dwumian $\left ( x-a \right )$ .

Wielomian $W(x)$ jest podzielny przez

dwumian $\left ( x-3 \right )$ ,

dwumian $\left ( x-6 \right )$ ,

ponieważ

liczba $x=3$ jest pierwiastkiem wielomianu.

wyraz wolny wielomianu jest równy $6$ .

liczba $x=6$ jest pierwiastkiem wielomianu.

ROZWIĄZANIE

zadanie 14 (0-2)

Rozwiąż nierówność. Podaj największa liczbę całkowitą spełniającą te nierówność.

$2x\geq \sqrt{5}\cdot x+3\sqrt{5}-6$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 15 (0-2)

Rozwiąż równanie

$-2x^3+x^2+18x-9=0$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 16 (0-3)

Rozwiąż równanie

$-x^3+13x-12=0$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 17 (0-4)

Szymon przygotowuje się do egzaminu na prawo jazdy. Opanował już $97$ spośród $3697$ zadań. Postanowił, że każdego kolejnego dani będzie rozwiązywał $n$ zadań. Zauważył, że gdyby dzienną liczbę rozwiązanych zadań zwiększył o $5$ , czas potrzebny na rozwiązanie wszystkich zadań skróciłby się o $10$ dni.

Oblicz ile dni zajmie Szymonowi przygotowanie do egzaminu, jeśli nie będzie zwiększał dziennej liczby rozwiązanych zadań.

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 18 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Równanie:

$\frac{\left ( 3x^2-6x \right )\left ( x^2-9 \right )}{\left ( x-2 \right )\left ( x-3 \right )^2}=0$

w zbiorze liczb rzeczywistych

A. nie ma rozwiązań.

B. ma dokładnie jedno rozwiązanie: $x=0$ .

C. ma dokładnie dwa rozwiązania: $x=0$ , $x=-3$ .

D. ma dokładnie cztery rozwiązania: $x=0$ , $x=2$ , $x=3$ , $x=-3$ .

ROZWIĄZANIE

zadanie 19 (0-2)

Niech $\frac{m}{n}$ będzie ułamkiem nieskracalnym. Jeśli do licznika dodamy $6$ , a do mianownika dodamy $15$ , jego wartość nie zmieni się.

Oblicz liczby $m$ i $n$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 20 (0-2)

Dane jest liczba dwucyfrowa $a$ , w której suma cyfr jest równa $14$ . Jeżeli zamienimy miejscami jej cyfry, otrzymamy liczbę o $18$ mniejsza od liczby sprzed tej zamiany cyfr.

Oblicz liczbę $a$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 21 (0-3)

Pies goni lisa. Początkowa odległość między zwierzętami była równa $30\; \mathrm{m}$ . Długość każdego skoku psa jest równa $2\; \mathrm{m}$ , długość każdego skoku lisa jest równa $1\; \mathrm{m}$ . W czasie, w którym lis wykonuje trzy skoki, pies skacze dwa razy.

Oblicz dystans, po przebiegnięciu którego pies dogoni lisa. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 22 (0-2)

Suma liczb rzeczywistych $a$ i $b$ równa jest $527$ . Wiemy, że $8%$ liczby $a$ jest równa $7,5%$ liczby $b$ .

Oblicz liczby $a$ i $b$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 23 (0-4)

Rozwiąż układ równań $\left\{\begin{matrix} x^2+y^2-4x+4y-17=0 & \\2x-y-1=0 & \end{matrix}\right.$

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 24 (0-2)

Dana jest funkcja kwadratowa $f$ określona wzorem

$y=f(x)=x^2+5x+6$ gdzie $x\in \mathbb{R}$

Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród D-H.

1. Postać kanoniczna funkcji $f$ wyraża się wzorem

A. $y=\left ( x-\frac{5}{2} \right )^2+\frac{1}{4}$

B. $y=\left ( x-\frac{5}{2} \right )^2-\frac{1}{4}$

C. $y=\left ( x-\frac{1}{4} \right )^2+\frac{5}{2}$

D. $y=\left ( x+\frac{1}{4} \right )^2-\frac{5}{2}$

2. Postać iloczynowa funkcji $f$ wyraża się wzorem

E. $y=\left ( x-2 \right )\left ( x-3 \right )$

F. $y=\left ( x-2 \right )\left ( x+3 \right )$

G. $y=\left ( x+2 \right )\left ( x-3 \right )$

H. $y=\left ( x+2 \right )\left ( x+3 \right )$

ROZWIĄZANIE

zadanie 25

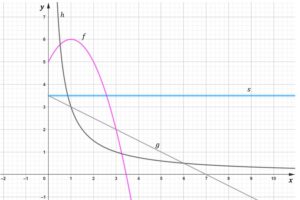W kartezjańskim układzie współrzędnych $\left ( x,y \right )$ przedstawiono fragmenty wykresów czterech funkcji: $f,g,h,s$ .

zadanie 25.1 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Największą wartość dla argumentu $x=2$ przyjmuje funkcja

A. $f$

B. $g$

C. $h$

D. $s$

ROZWIĄZANIE

zadanie 25.2 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Dla argumentu $x=3$ tę samą wartość przyjmuje funkcja

A. $f$ i $s$

B. $s$ i $h$

C. $f$ i $g$

D. $g$ i $s$

ROZWIĄZANIE

zadanie 25.3 (0-1)

Zapisz maksymalny przedział, w którym prawdziwa jest nierówność $g(x)>h(x)$ .

……………………………………………………………………………………………………………………………………………………….

ROZWIĄZANIE

zadanie 26

Temperatura powietrza obniża się wraz ze wzrostem wysokości n.p.m. Na postawie danych empirycznych stwierdzono, że temperatura maleje o $0,6^\circ C$ , gdy wysokość wzrasta o $100\; \mathrm{m}$ , a wysokość maleje o $100\; \mathrm{m}$ – temperatura rośnie o $0,6^\circ C$ . W Zakopanem, które znajduje się na wysokości $1000$ metrów n.p.m., temperatura powietrza zmierzona w punkcie pomiarowym była równa $13^\circ C$ . W tym samym czasie dokonano pomiarów temperatury powietrza w Białce Tatrzańskiej i na Rysach.

zadanie 26.1 (0-1)

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Na Rysach, na wysokości $2499$ metrów n.p.m., zmierzona temperatura powietrza nie przekraczała $5^\circ C$ .	P	F
W Białce Tatrzańskiej ( $650$ metrów n.p.m.) zmierzona temperatura powietrza była równa $16,5^\circ C$ .	P	F

ROZWIĄZANIE

zadanie 26.2 (0-2)

Niech $f(x)=ax+b$ będzie funkcją opisującą zależność temperatury powietrza od wysokości $x$ n.p.m. w dowolnym punkcie nad Zakopanem.

Oblicz wartość współczynnika $a$ i wartość współczynnika $b$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 27 (0-1)

Funkcja kwadratowa $f$ jest określona wzorem $f(x)=-2x^2+bx+c$ i przyjmuje wartości dodatnie tylko dla $x\in \left ( -4,2 \right )$ .

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Osią symetrii paraboli będącej wykresem tej funkcji jest prosta $x=1$ .	P	F
Postać iloczynowa funkcji $f$ wyraża się wzorem $f(x)=-2(x+4)\left ( x-2 \right )$ .	P	F

ROZWIĄZANIE

zadanie 28 (0-2)

Dana jest funkcja kwadratowa $f$ . Do wykresu tej funkcji należy punkt o współrzędnych $(0,8)$ , a osią symetrii jej wykresu jest prosta o równaniu $x=4$ . Jednym z miejsc zerowych funkcji $f$ jest $x_{1}=2$ .

Wyznacz i zapisz wzór funkcji $y=f(x)$ w postaci iloczynowej.

ROZWIĄZANIE

zadanie 29 (0-1)

Aby zaorać pole o powierzchni $P$ w ciągu $8$ godzin, potrzeba trzech ciągników. Przyjmijmy, że każdy ciągnik w ustalonej jednostce czasu może zaorać tę sama powierzchnie pola.

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Zaoranie pola o powierzchni $P$ przy pomocy dwóch ciągników zajęłoby $12$ godzin.	P	F
Cztery ciągniki, które pracują o połowę szybciej, zaorały by to pole w ciągu $4$ godzin.	P	F

ROZWIĄZANIE

zadanie 30 (0-1)

Dane są liczby $a=2\sqrt{2}$ , $b=4$ , $c=4\sqrt{2}$ .

Dokończ zdanie tak aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.

Liczby $a,b$ oraz $c$ tworzą w podanej kolejności

ciąg arytmetyczny,

ciąg geometryczny,

ponieważ

$b=\frac{a+c}{2}$

$b=\frac{\left ( c-a \right )^2}{2}$

$b^2=a\cdot c$

ROZWIĄZANIE

zadanie 31 (0-2)

Dany jest ciąg arytmetyczny $\left ( a_{n} \right )$ określony dla każdej liczby naturalnej $n\geq 1$ . Jego różnica jest równa $4$ , a suma jego pierwszych wyrazów jest trzy razy mniejsza od sumy następnych pięciu wyrazów.

Oblicz pierwszy wyraz tego ciągu. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 32 (0-3)

Iloraz skończonego ciągu geometrycznego jest równy $\frac{1}{3}$ , trzeci wyraz tego ciągu jest równy $\frac{1}{9}$ , a suma wszystkich wyrazów to $\frac{364}{243}$ .

Oblicz, z ilu wyrazów składa się ten ciąg. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 33 (0-4)

Liczby $x,y,z$ , których suma jest równa $114$ , tworzą w podanej kolejności ciąg geometryczny. Liczby te są również wyrazami pewnego ciągu arytmetycznego $(a_{n})$ gdzie $n\geq 1$ , w którym $x=a_{1}$ , $y=a_{4}$ i $z=a_{25}$ .

Oblicz liczby $x,y,z$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 34 (0-4)

Te liczby, których suma jest równa $24$ , tworzą ciąg arytmetyczny. Po zwiększeniu ich odpowiednio o $4,10$ i $40$ będą w tej samej kolejności tworzyły ciąg geometryczny.

Oblicz te trzy liczby tworzące ciąg arytmetyczny. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 35

Pani Joanna postanowiła systematycznie oszczędzać i co miesiąc na swoje subkonto odkładać pewną sumę pieniędzy. Pierwszego czerwca 2020 roku wpłaciła $300$ złotych. Pierwszego dnia każdego miesiąca wpłacała o $25$ zł więcej niż w miesiącu poprzednim.

zadanie 35.1 (0-1)

Oblicz kwotę jaką pani Joanna wpłaciła na subkonto pierwszego czerwca 2022.

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 35.2 (0-2)

Zapisz, o ile większą kwotę niż w miesiącu poprzednim pani Joanna powinna odkładać, aby pierwszego czerwca 2025 roku (uwzględniając również wpłatę w tym dniu) na subkoncie była kwota 76 860 złotych.

Zapisz obliczenia.

ROZWIĄZANIE

zadanie 36 (0-3)

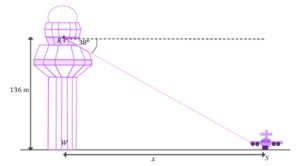Z okna wieży kontroli lotów widać startujący samolot $S$ pod kątem $38^\circ$ do poziomu. Kontroler $K$ znajduje się na wysokości $136\; \mathrm{m}$ od płyty lotniska (zobacz rysunek).

Oblicz odległość $x$ samolotu $S$ od podstawy $W$ tej wieży.

Wynik podaj w zaokrągleniu do pełnych metrów. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 37

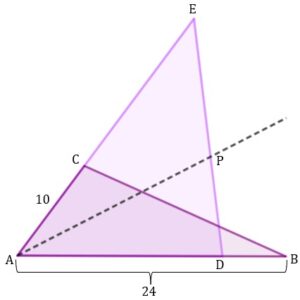Dane są dwa trójkąty $ABC$ i $ADE$ o wspólnym kącie ostrym przy wierzchołku $A$ . Ponadto $\left | AB \right |=24$ , $\left | AC \right |=10$ (zobacz rysunek). Pole trójkąta $ADE$ jest dwukrotnie większe od pola trójkąta $ABC$ .

zadanie 37.1 (0-2)

Dwusieczna kąta $BAC$ przecina odcinek $DE$ w punkcie $P$ , takim że $\frac{\left | DP \right |}{\left | PE \right |}=\frac{3}{4}$ .

Oblicz długość boków $AD$ i $AE$ trójkąta $ADE$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 37.2 (0-3)

Pole trójkąta $ABC$ jest równe $72$ .

Oblicz długość boku $BC$ trójkąta $ABC$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 38 (0-2)

Dany jest trójkąt równoramienny, który nie jest równoboczny. Punkt $O$ jest środkiem okręgu opisanego na tym trójkącie, a punkt $H$ jest jego ortocentrum .

Wybierz dwie właściwe odpowiedzi spośród podanych.

A. Punkt $O$ jest równo oddalony tylko od dwóch wierzchołków tego trójkąta.

B. Punkt $O$ jest równo oddalony od trzech wierzchołków tego trójkąta.

C. Punkt $O$ jest równo oddalony od trzech boków tego trójkąta.

D. Punkt $H$ jest równo oddalony tylko od dwóch wierzchołków tego trójkąta.

E. Punkt $H$ jest równo oddalony od trzech wierzchołków tego trójkąta.

F. Punkt $H$ jest równo oddalony od trzech boków tego trójkąta.

ROZWIĄZANIE

zadanie 39 (0-1)

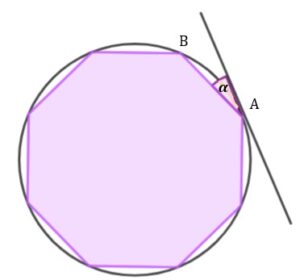Dany jest ośmiokąt foremny wpisany w okrąg $K$ . Punkty $A$ oraz $B$ są sąsiednimi wierzchołkami tego ośmiokąta oraz $\alpha$ jest kątem między styczną do okręgu $K$ w punkcie $A$ i bokiem $AB$ wielokąta (zobacz rysunek).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Miara kąta $\alpha$ jest równa

A. $45^\circ$

B. $30^\circ$

C. $22,5^\circ$

D. $15^\circ$

ROZWIĄZANIE

zadanie 40 (0-1)

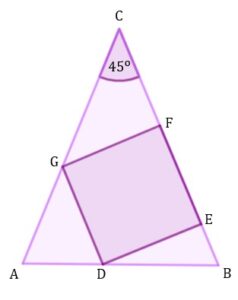Dane są trójkąt równoramienny $ABC$ , w którym $\left | AC \right |=\left | BC \right |$ i $\left | \measuredangle ACB \right |=45^\circ$ oraz kwadrat $DEFG$ o polu równym $1$ . Wierzchołki $E$ i $F$ kwadratu leżą na ramieniu $BC$ danego trójkąta, wierzchołek $G$ leży na ramieniu $AC$ , a wierzchołek $D$ leży na podstawie $AB$ trójkąta (zobacz rysunek).

Oceń prawdziwość podanych relacji. Wybierz P, jeśli relacja jest prawdziwa, albo F – jeśli jest fałszywa.

$\left \| \measuredangle AGD\right \|=45^\circ$	P	F
$\left \| AG \right \|-\left \| BE \right \|=2-\sqrt{2}$	P	F

ROZWIĄZANIE

zadanie 41 (0-2)

Dane są:

okrąg o środku $S$ i promieniu $r=1$
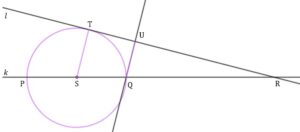prosta $k$ przechodząca przez $S$ i przecinająca okrąg w punktach $P$ i $Q$
prosta $l$ styczna do okręgu w punkcie $T$ .

Prosta $k$ przecina prostą $l$ w punkcie $R$ . Prosta przechodząca przez punkt $Q$ i równoległa do odcinka $ST$ przecina styczną $l$ w punkcie $U$ (zobacz rysunek).

Oblicz długość odcinka $TU$ wiedząc, że spełniony jest warunek $\frac{\left | PQ \right |}{\left | QR \right |}=\frac{2}{3}$ .

Zapisz obliczenia.

ROZWIĄZANIE

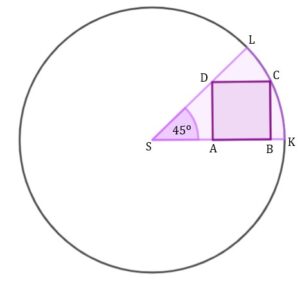
zadanie 42 (0-3)

W wycinek koła wyznaczony przez kąt środkowy $KSL$ o mierze $45^\circ$ wpisano kwadrat $ABCD$ w taki sposób, że wierzchołki $A$ oraz $B$ leżą na promieniu $SK$ , wierzchołek $D$ leży na promieniu $SL$ , a wierzchołek $C$ leży na łuku $\widehat{KL}$ (zobacz rysunek).

Oblicz stosunek pola kwadratu $ABCD$ do pola wycinka kołowego $KSL$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 43 (0-4)

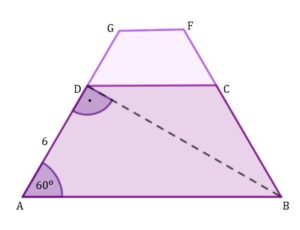Dany jest trapez równoramienny $ABCD$ o podstawach $AB$ i $CD$ , o podstawach $\left | AB \right |$ i $\left | CD \right |$ , gdzie $\left | AB \right |> \left | CD \right |$ . Kąt ostry tego trapezu ma miarę $60^\circ$ , a przekątna jest prostopadła do ramienia, którego długość jest $6$ . Oba ramiona tego trapezu przedłużono, otrzymując trapez $DCFG$ podobny do trapezu $ABCD$ (zobacz rysunek).

Oblicz pole trapezu $DCFG$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 44 (0-2)

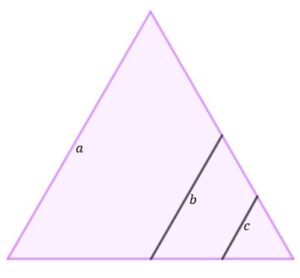W trójkącie równobocznym o boku długości $a$ poprowadzono dwa odcinki równoległe do jednego z jego boków. Długości tych odcinków są równe $b$ i $c$ , przy czym $c< b< a$ (zobacz rysunek). Odcinki podzieliły trójkąt równoboczny na trzy figury: dwa trapezy i trójkąt.

Wykaż, że stosunek pola trapezu o podstawach $b$ i $c$ do pola trapezu o postawach $a$ i $b$ jest równy $\frac{b^2-c^2}{a^2-b^2}$ .

ROZWIĄZANIE

zadanie 45 (0-1)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , rozważamy dwie proste o równaniach

$y=a+b\cdot x$ oraz $y=-\frac{1}{a}-\frac{2}{3}b^2\cdot x$

gdzie $a\neq 0$ , $b\neq 0$ .

Dokończ zdanie tak aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.

Dla $a=2$ i $b=-\frac{3}{2}$ rozważane proste są

prostopadłe,

równoległe,

ponieważ

$a\cdot \left (-\frac{1}{a} \right )=-1$

$\left ( a+b \right )\left ( -\frac{1}{a}-\frac{2}{3}b^2 \right )=-1$

$b=-\frac{2}{3}b^2$

ROZWIĄZANIE

zadanie 46

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest trójkąt $ABC$ . Wierzchołki tego trójkąta mają współrzędne: $A=(-15,-8)$ , $B=(-6,4)$ , $C=(-19,-5)$ .

zadanie 46.1 (0-2)

Wykaż, że trójkąt $ABC$ jest prostokątny. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 46.2 (0-3)

Wierzchołki trójkąta $ABC$ są trzema wierzchołkami równoległoboku $ABCD$ . Odcinek $AC$ jest przekątną tego równoległoboku.

Oblicz współrzędne wierzchołka $D$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 46.3 (0-1)

Uzupełnij zdanie. Wpisz odpowiednie liczby w zaznaczonych miejscach, aby zdanie było prawdziwe.

Punkt $S$ przecięcia środkowych trójkąta $ABC$ ma współrzędne $S=\left ( ........,........ \right )$ .

ROZWIĄZANIE

zadanie 47 (0-1)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest okrąg $O$ o równaniu $x^2+y^2=2$ oraz prosta $k$ o równaniu $y=m$ , gdzie $m\in \mathbb{R}$ .

Uzupełnij zdanie. Wpisz odpowiedni przedział w wykropkowanym miejscu, aby zdanie było prawdziwe.

Okrąg $O$ i prosta $k$ mają dwa punkty wspólne, tylko wtedy, gdy $m\in ................$

ROZWIĄZANIE

zadanie 48 (0-4)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , dany jest trójkąt $ABC$ . Podstawa $AB$ tego trójkąta zawiera się w prostej o równaniu $y=-3x+6$ . Wierzchołki $A$ i $B$ leżą – odpowiednio – na osi $Oy$ oraz $Oy$ . Wierzchołek $C$ ma współrzędne $(3,7)$ .

Oblicz pole trójkąta $ABC$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 49 (0-4)

Na płaszczyźnie w kartezjańskim układzie współrzędnych $\left ( x,y \right )$ , punkty $A=(-8,12)$ i $B=(-2,4)$ są końcami cięciwy okręgu $O$ . środek tego okręgu leży na prostej $k$ o równaniu $y=4x+2$ .

Wyznacz współrzędne środka okręgu $O$ i promień tego okręgu. Zapisz obliczenia.

ROZWIĄZANIE

zadanie 50 (0-3)

Funkcja kwadratowa $f$ określona jest wzorem $f(x)=-x^2+2x+3$ . Funkcja liniowa $g$ określona jest wzorem $g(x)=-x+5$

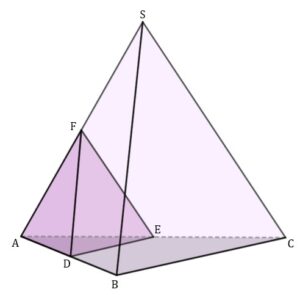
Oblicz współrzędne punktów, w których przecinają się wykresy funkcji $y=f(x)$ oraz funkcji $y=g(x)$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 51 (0-2)

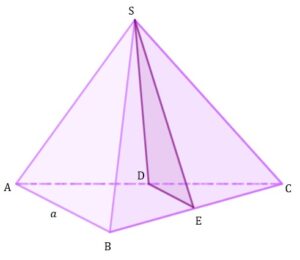Każda krawędź czworościanu $ABCS$ ma długość $a$ . Punkty $D$ i $E$ są środkami boków – odpowiednio – $AC$ oraz $BC$ (zobacz rysunek).
Oblicz pole trójkąta $DES$ . Zapisz obliczenia.

ROZWIĄZANIE

zadanie 52 (0-2)

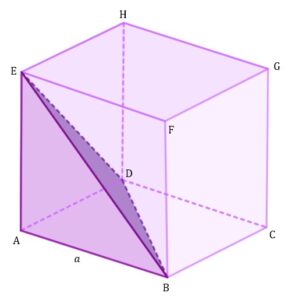Dany jest sześcian $ABCDEFGH$ o krawędzi długości $a$ . Punkty $A,B,D$ i $E$ są wierzchołkami ostrosłupa (zobacz rysunek).
Oblicz pole powierzchni ostrosłupa $ABDE$ .
Zapisz obliczenia.

ROZWIĄZANIE

zadanie 53 (0-2)

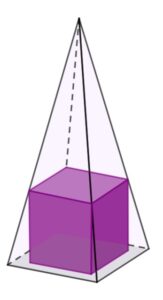Dany jest ostrosłup prawidłowy czworokątny o krawędzi długości $2$ i wysokości $8$ . Wpisano w niego sześcian w taki sposób, że dolna podstawa sześcianu zawiera się w podstawie ostrosłupa, a krawędzie jego górnej podstawy zawierają się w ścianach bocznych ostrosłupa (zobacz rysunek).

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

1.	Krawędź sześcianu jest dłuższa niż $1,5$ .	P	F
2.	Ostrosłup jest czterokrotnie wyższy od sześcianu.	P	F
3.	Objętość sześcianu jest większa od $4$ .	P	F

ROZWIĄZANIE

zadanie 54 (0-1)

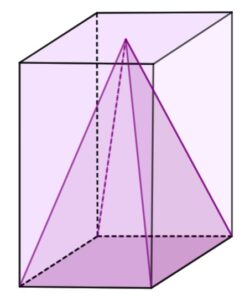Dany jest graniastosłup prawidłowy czworokątny, o krawędzi podstawy $a$ oraz wysokości $h$ . Wpisano w niego ostrosłup prawidłowy czworokątny w taki sposób, że krawędzie podstawy ostrosłupa i graniastosłupa pokrywają się, zaś górny wierzchołek ostrosłupa jest środkiem podstawy górnej graniastosłupa (zobacz rysunek).

Niech $F$ będzie bryłą powstałą po wycięciu ostrosłupa z graniastosłupa.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Różnica objętości bryły $F$ i objętości ostrosłupa jest równa

A. $\frac{1}{3}a^2h$

B. $\frac{2}{3}a^2h$

C. $\frac{1}{3}ah^2$

D. $\frac{2}{3}ah^2$

ROZWIĄZANIE

zadanie 55 (0-1)

W ostrosłupie prawidłowym trójkątnym $ABCS$ zaznaczono środki krawędzi $AB,AC$ i $AS$ odpowiednio punktami $D,E,F$ (zobacz rysunek)

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Pole powierzchni ostrosłupa $ADEF$ jest dwukrotnie mniejsze od pola powierzchni ostrosłupa $ABCS$ .	P	F
Objętość ostrosłupa $ADEF$ jest ośmiokrotnie mniejsza od objętości ostrosłupa $ABCS$ .	P	F

ROZWIĄZANIE

zadanie 56 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich liczb naturalnych trzycyfrowych, w zapisie których cyfra $5$ występuje dokładnie jeden raz, jest

A. $125$

B. $225$

C. $280$

D. $300$

ROZWIĄZANIE

zadanie 57 (0-1)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej $3$ jest

A. $3$

B. $5$

C. $6$

D. $10$

ROZWIĄZANIE

zadanie 58 (0-1)

Na dwóch półkach ustawiono $9$ książek: $4$ biograficzne i $3$ fantasy. Ustawiono je w taki sposób, aby na każdej półce znalazły sie książki wyłącznie jednego rodzaju.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wszystkich sposobów ustawienia książek przy zadanym warunku jest

A. $4!\cdot 5!\cdot 2$

B. $4!\cdot 5!$

C. $4\cdot 5$

D. $4\cdot 5\cdot 2$

ROZWIĄZANIE

zadanie 59 (0-1)

Firma krawiecka produkuje prostokątne dwukolorowe obrusy w jednakowym rozmiarze. Każdy obrus jest zszyty z trzech pasów materiału tej samej szerokości (zobacz rysunek). Zewnętrzne pasy są w tym samym kolorze. Cały obrus jest obszyty lamówką w jednym kolorze. W firmowym magazynie materiały są dostępne w $5$ kolorach, a lamówka – w trzech kolorach. Obrusy uznajemy za różne, gdy różnią się kolorem lamówki lub kolorem pasów zewnętrznych, lub kolorem pasa wewnętrznego.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba wszystkich różnych obrusów, które może produkować, jest równa

A. $5\cdot 3\cdot 4$

B. $5\cdot 5\cdot 3$

C. $5\cdot 5\cdot 5\cdot 3$

D. $5\cdot 4\cdot 3\cdot 3$

ROZWIĄZANIE

zadanie 60 (0-2)

Do dyspozycji są dwa puste pojemniki oraz pięć kul. Każdą z kul należy umieścić w pojemniku. Liczba wszystkich różnych rozmieszczeń tych kul zależy od cech kul i pojemników.

W poniższej tabeli w lewej kolumnie podano cechy obiektów (kul i pojemników).

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwa odpowiedź wybraną spośród A-F.

Cechy kul i pojemników	Liczba wszystkich różnych rozmieszczeń kul w pojemnikach
Kule rozróżnialne, pojemniki rozróżnialne
Kule rozróżnialne, pojemniki nierozróżnialne
Kule nierozróżnialne, pojemniki rozróżnialne
Kule nierozróżnialne, pojemniki nierozróżnialne

A. $6$	B. $2\cdot 5$
C. $2^4$	D. $3$
E. $2^5$	F. $5^2$

ROZWIĄZANIE

zadanie 61 (0-1)

Średnia arytmetyczna wieku czterech kobiet jest równa $24$ lata. Średnia arytmetyczna wieku sześciu mężczyzn jest równa $26$ lat.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Średnia arytmetyczna wieku tych dziesięciu osób jest równa

A. $25$

B. $25,2$

C. $24,9$

D. $25,5$

ROZWIĄZANIE

zadanie 62 (0-1)

Mediana zestawu sześciu liczb $1,2,3,4,5,2x$ jest równa $3$

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba $x$ jest równa

A. $1$

B. $1,5$

C. $2$

D. $3$

ROZWIĄZANIE

zadanie 63 (0-1)

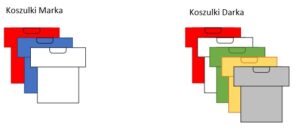Marek ma $3$ koszulki w kolorach czerwonym, niebieskim i białym. Darek ma $5$ koszulek w kolorach czerwonym, białym, zielonym, żółtym i szarym. Chłopcy umówili się, że następnego dnia każdy z nich założy wybrana w sposób losowy jedną ze swoich koszulek.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Prawdopodobieństwo zdarzenia polegającego na tym, że następnego dnia chłopcy założą koszulki w tym samym kolorze, jest równe

A. $\frac{2}{15}$

B. $\frac{3}{5}$

C. $\frac{2}{5}$

D. $\frac{4}{15}$

ROZWIĄZANIE

zadanie 64 (0-1)

Dany jest pięciokąt foremny $ABCDE$ . Losujemy jednocześnie dwa różne wierzchołki tego pięciokąta.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane wierzchołki będą końcami przekątnej pięciokąta $ABCDE$ , jest równe

A. $\frac{3}{10}$

B. $\frac{3}{5}$

C. $\frac{2}{5}$

D. $\frac{1}{2}$

ROZWIĄZANIE

zadanie 65 (0-1)

Ze zbioru pięciu liczb $\left \{ 1,2,3,4,5 \right \}$ losujemy dwa razy po jednej liczbie ze zwracaniem.

Oceń prawdziwość podanych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie parzysta, jest równa $\frac{8}{25}$ .	P	F
Prawdopodobieństwo zdarzenia polegającego na tym, że obie liczby będą parzyste, jest równe $\frac{2}{25}$ .	P	F

ROZWIĄZANIE

zadanie 66 (0-3)

Firma handlowa ustaliła, że liczba sprzedanych przez nią egzemplarzy gry komputerowej w ciągu każdego tygodnia zależy od jej ceny. Liczbę sprzedanych egzemplarzy opisuje funkcja $f(x)=2400-15x$ , gdzie $x$ oznacza cenę jednostkową gry.

Jaka powinna być cena jednostkowa, aby tygodniowy przychód $P$ ze sprzedaży gry był największy? Oblicz ten największy przychód.

Zapisz obliczenia.

Wskazówka: przyjmij, że przychód jest iloczynem liczby sprzedanych gier oraz ceny jednostkowej tej gry.

ROZWIĄZANIE

zadanie 67 (0-4)

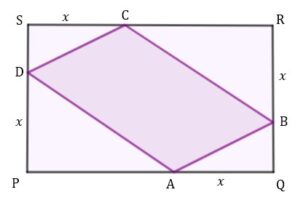Wyznacz długość odcinaka $x$ , dla którego pole czworokąta $ABCD$ jest najmniejsze.

Wyznacz to pole. Zapisz obliczenia.

ROZWIĄZANIE

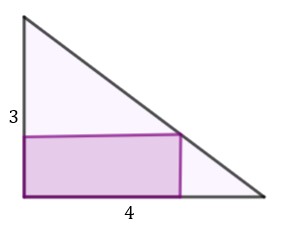
zadanie 68 (0-4)

Dany jest trójkąt prostokątny o przyprostokątnych $3$ i $4$ . Wpisano w niego prostokąt w taki sposób, że dwa z jego boków zawierają się w przyprostokątnych trójkąta, a jeden wierzchołek leży na przeciwprostokątnej (zobacz rysunek).

Jakie wymiary powinien mieć prostokąt aby jego pole było największe?

Oblicz to największe pole. Zapisz obliczenia.

ROZWIĄZANIE

Was this helpful?

0 / 0